Exploring Quantum Computing

As I was sitting in front of my computer one day, I found myself thinking about the future of computers, which led to me thinking about quantum computing. I realized I really didn’t know much about the concept of quantum computing, and that led me to explore my curiosity and do some research.

Quantum computing sounds really cool. We’ve all read about the massive investments that have been made in making it a reality, and it has a lot of potential to make breakthroughs in many industries. One thing I found is that the news about quantum computing often glosses over what it is and how it works. I came to find that it was for a reason: quantum computing is very different from “normal” digital computing and it requires thinking about things in a non-intuitive way. Plus, there’s a lot of math involved.

Quantum Computing Concepts

Quantum computers use qubits instead of the traditional bits (binary digits) that our computers currently use. Qubits are different from traditional bits, because until they are read out (measured), they can exist in an indeterminate state, where we can’t tell whether or not they’ll be measured as a 0 or a 1. That’s due to a unique property, called superposition.

Now, superposition certainly makes qubits interesting, but the really interesting phenomenon is entanglement. Entangled qubits can interact instantly. In order to make functional qubits, quantum computers must be cooled to near absolute zero. Even when supercooled, qubits don’t maintain their entangled state for very long.

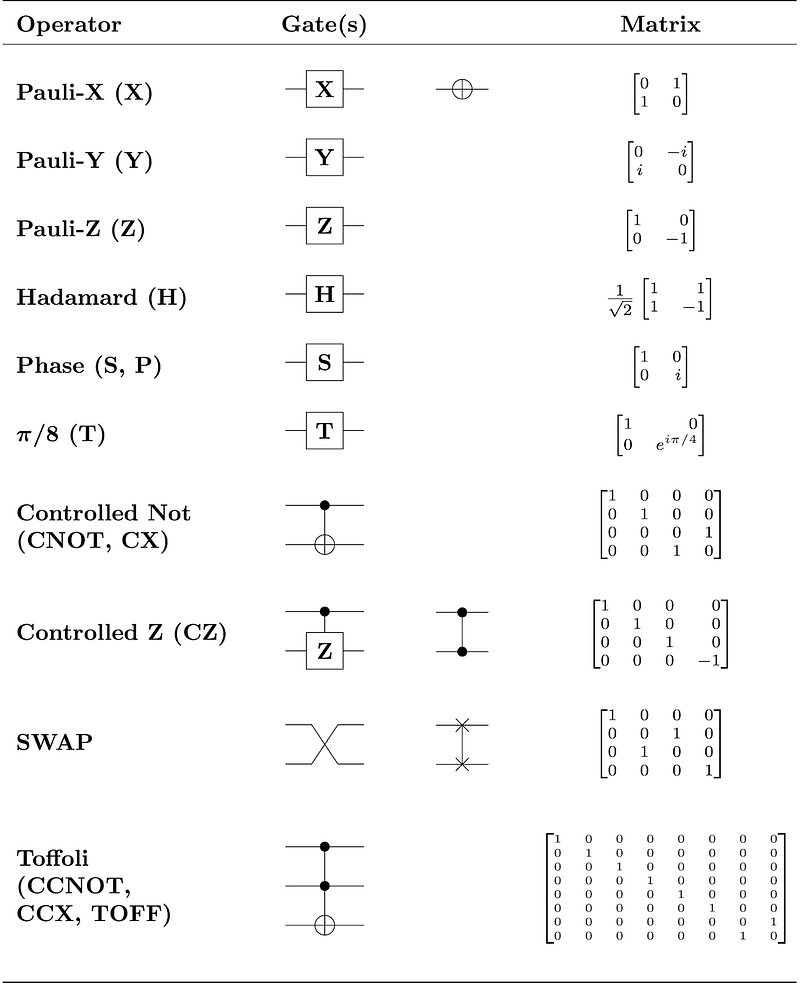
This makes programming them rather difficult. Quantum computers are programmed using different sequences of various kinds of logic gates, but the programs must run quickly enough that the qubits don’t lose coherence before they are measured. People who may have taken a logic class, or looked at building circuits using flip-flops, could find quantum logic gates somewhat familiar, although quantum computers themselves are essentially analog. However, the combination of entanglement and superposition make the process a lot more confusing.

Qubits & Superposition

The ordinary bits we use in everyday digital computers are either 0 or 1. They can be read whenever you want, and unless there is a hardware issue, they won’t change. However, qubits don’t behave like that. They have a probability of being 0 and a probability of being 1, but until they are measured, they may be in an indefinite state. That state, along with some other state information that can allow for more computational complexity, can be described as being an arbitrary point on a sphere (of radius 1) that reflects both the probability of being measured as a 0 or 1 (which are the north & south poles).

The qubit’s state is a combination of the values along all three axes. This is superposition. Some articles describe this property as “being in all possible states at the same time”, while others feel that’s somewhat misleading, and that we’re better off with the probability explanation. Either way, a quantum computer can actually perform math operations on the qubit while it’s in superposition (modifying the probabilities in various ways through logic gates) before eventually outputting a result by measuring it. In all cases, though, once a qubit is read, it is either 1 or 0, and it loses its other state information.

Qubits generally start life at 0, although they are frequently then moved into an indeterminate state using a Hadamard Gate, which results in a qubit that will read out as 0 half the time, and 1 the other half. Other gates are also available to flip the state of a qubit by varying amounts and directions, both relative to the 0 and 1 axes, and also a third axis that represents phase, and provides additional possibilities for representing information. However, the specific gates & operations available depend on the quantum computer and toolkit being used.

Entanglement

Groups of independent qubits, by themselves, aren’t powerful enough to create the massive breakthroughs that are promised by quantum computing. The magic really begins to happen when the concept of quantum entanglement is introduced. One industry expert likened qubits without entanglement as being like a “very expensive classical computer.” Entangled qubits affect each other instantly when measured, no matter how far apart they are. In terms of classic computing, this is almost like having a logic gate connecting every bit in memory to every other bit.

You can start to see how powerful that might be, compared to a traditional computer needing to read and write from each element of memory separately before being able to operate on it. As a result of this, there are some very large gains that become possible from entanglement. The first is a large increase in the complexity of programming that could be executed, at least for certain types of problems. Another one is the modeling of complex molecules and materials that are extremely difficult to simulate with classical computers. Another could be innovations in long-distance secured communication, if and when it becomes possible to preserve quantum state over large distances. Programming using entanglement usually starts with the C-NOT gate, which flips the state of an entangled particle if its partner is read out as a 1. This is somewhat like a traditional XOR gate, except for the fact that it only operates when a measurement is made.

Quantum computers and cryptography

Superposition and entanglement are impressive phenomena, but leveraging them to do computation requires a very different mindset and programming model. You can’t just throw your Python code on a quantum computer and expect it to run, and certainly not to run faster. Fortunately, mathematicians and physicists were thinking ahead, and developed algorithms that take advantage of quantum computers decades before the machines even started to appear.

I remember reading about the fact that quantum computers one day could break most cryptography systems. They will be able to do this because there are some algorithms design to run on quantum computers that can solve a hard math problem, which can then, in turn, be used to factor very large numbers. One of the most famous examples of this is Shor’s Factoring Algorithm. The difficulty of factoring large numbers is essential to the security of all public-private key systems, which are the most commonly used system today. Current quantum computers don’t have nearly enough qubits to attempt the task, but several experts predict they will, within the next 3–8 years. This leads to some potentially dangerous situations, such as if only governments and the extremely-rich had access to the ultra-secure encryption provided by quantum computers.

Why is building quantum computers so hard?

There are a bunch of reasons quantum computers are taking a long time to develop. To start, you need to find a way to isolate and control a physical object that implements a qubit. Part of that process also requires cooling it to nearly absolute zero (in the case of IBM’s Quantum One, it is cooled to .015° K). Even with this extreme cooling, qubits are only stable for a very short amount of time, which greatly limits the flexibility of programmers in how many operations they can perform before needing to read out a result.

Not only do programs need to be constrained, but they also need to be run several times, as current qubit implementations have a pretty high error rate. Additionally, entanglement isn’t easy to implement in hardware either. In many designs, only some of the qubits are entangled, so the computer needs to have the ability to swap bits around as needed to help simulate a system where all the bits can potentially be entangled.

Moore’s Law

You may have heard about something called Moore’s Law, which is “the observation that the number of transistors in a dense integrated circuit doubles about every two years”. The “law” is in fact just an empirical relationship, and not a physical or natural law. It was named after Gordon Moore, the CEO and co-founder of Intel, whose 1965 paper described a 2x increase in the number of components per integrated circuit per year, and he projected this rate of growth would continue for at least another decade. In 1975, he revised the forecast to doubling every 2 years. This prediction ended up being used in the semiconductor industry to guide long-term planning, and to set targets for research and development. As of 2018, leading semiconductor manufacturers have integrated circuit fabrication processed in mass production with 10 nm and 7 nm features, which keep pace with Moore’s law.

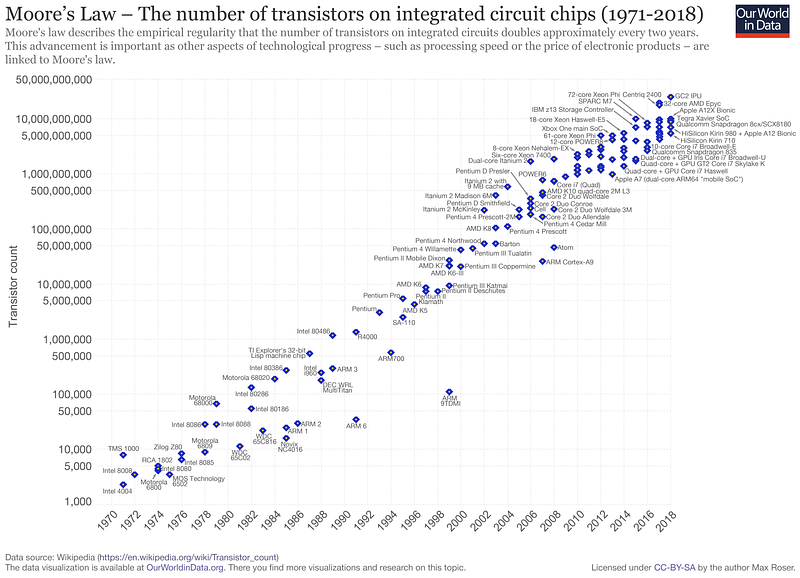
However, with quantum computers this law doesn’t make sense. According to an article by Quanta Magazine, this led to the creation of a new idea, known as Neven’s Law. The law, named after Hartmut Neven, the director of the Quantum Artificial Intelligence Lab at Google, who first discovered the phenomenon, dictates how quickly quantum processors are improving, relative to traditional digital computers.

As it turns out, they’re gaining on ordinary computers at an extremely fast, “doubly exponential rate”. This means that processing power grows by a factor of 2^2^1(4), then 2^2^2 (16), then 2^2^3 (256), then 2^2^4 (65,536), and so on. With this model, as you can see, numbers get mind-bogglingly big very, very fast. Doubly-exponential growth is so fast, it’s hard to find anything that grows so quickly in the natural world, according to Quanta.

Based on this observation, Neven suggested that quantum supremacy could occur in 2019. Quantum supremacy is defined as “the goal of demonstrating that a programmable quantum device can solve a problem that no classical computer can feasibly solve.” Sure enough, in October 2019, Google declared quantum supremacy, on target with Neven’s prediction.

Overall, quantum computing is a very interesting field, and I’m looking forward to seeing what the future holds for us. What are your thoughts about quantum computing?